신경망, 딥러닝 개념은 다른 수치해석적 기법들에 비해 비교적 단순하며, 유용하다. 이 글은 딥러닝 종류, 활용, 개발 방법을 간략히 요약하였다. 종류, 활용 부분은 개념을 잘 표현하고 있다고 생각하는 레퍼런스들을 참고하였고, 개발 부분은 딥러닝 레퍼런스(김성필, wikibooks 등)에서 핵심 내용을 요약하였다. 좀 더 깊은 이해가 필요하다면, 본문에 인용된 레퍼런스들을 참고하길 바란다.
1. 딥러닝 종류 및 활용
딥러닝은 응용 목적별로 다양한 신경망으로 발전하고 있다.
1. 컨볼루션 뉴럴 네트워크
컨볼루션 뉴럴 네트워크(CNN. convolutional neural network)는 특징맵을 생성하는 필터까지도 학습이 가능해 비전(vision) 분야에서 성능이 우수하다.
CNN 기반 동물 이미지 학습 분류(PyImageSearch)
2. 순환신경망
순차적 정보가 담긴 데이터에서 규칙적인 패턴을 인식하고, 추상화된 정보를 추출할 수 있는 순환신경망(RNN. Recurrent Neural Network)은 텍스트, 음성, 음악, 영상 등 순차적 데이터를 다루는 데 적합하다. RNN은 그레디언트 소실 문제(Gradient Vanishing Problem)가 있어 패턴 학습을 못하는 경우가 있다. 이를 개선하기 위해, LSTM(Long Short Term Memory)가 개발되었다. RNN문제는 LSTM으로 어느정도 해결되어, 자동 작곡, 작사, 저술, 주가 예측 등 다양한 분야에 활용되고 있다.
LSTM 기반 음악 작곡(LSTM RNN Music Composition)
3. RBM 과 DBN
Geoff Hinton에 제안한 제한된 볼츠만 머신(RBM. Restricted Boltzmann Machine)은 비지도 학습에 활용되며, 차원 축소, 분류, 선형 회귀 분석, 필터링, 특징값 학습, 주제 모델렝에 사용할 수 있는 알고리즘이다. RBM은 undirected graph 구조이며, 노드 출력값은 확률값이다. RBM은 확률은 에너지 함수 형태로 표현되며, 에너지가 최소화되는 방향으로 학습하며, DBM을 구성하는 기본 요소이다.
RBM과 DBN 신경망 구조(Unsupervied Learning, patrickhebron.com)
DBN기반 나뭇잎 이미지 훈련(Unsupervied Learning, patrickhebron.com)
GAN(Generative Adversarial Network. 생성 대립 신경망)은 비지도 학습 방법으로 훈련으로 학습된 패턴을 이용해, 이미지나 음성을 생성할 수 있다. GAN은 이미지 및 음성 복원 등에 적용되었다. DCGAN(Deep Convolution GAN)은 불안정한 GAN 구조를 개선해 새로운 의미를 가진 이미지를 생성할 수 있다.
DCGAN(Unsupervied Representation Learning with Deep Convolutional Generative Adversarial Network, 2016)
5. RL
최근 구글의 딥마인드에서 개발한 관계형 네트워크(RL. Relation Networks)는 관계형 추론을 지원한다. RL을 통해, 물리적 사물, 문장, 추상적인 아이디어 들 사이에 관계를 파악해, 논리적 추론을 할 수 있다(손경호, 2017, ZDNet). 구글 딥마인드 팀은 RN을 이용해 주어진 장면을 학습시키면, 테이블 위 여러개 사각형, 구 등 다양한 모양으로 이뤄진 사물간 관계를 추론하는 데 성공하였다.
RL기반 객체 간 관계 추론(A simple neural network module for relational reasoning. 참고. Keras 머신러닝 플랫폼 RL 구현 소스)
지금까지 딥러닝은 분류, 이미지 인식, 음성 인식, 번역, 이미지 생성에만 국한된 한계가 있었다. RL는 딥러닝 기술을 인간의 사고에 근사한 논리적 추론이 가능한 분야까지 확대하였다.
여기서는 대표적인 딥러닝 신경망 모델만 설명하였다. 참고로, 응용 목적에 따라 다음 그림과 같이 다양한 신경망 모델이 있다.
- THE NEURAL NETWORK ZOO
- The 9 Deep Learning Papers You Need To Know About CNN
- My Top 9 Favorite Python Deep Learning Libraries
앞으로 딥러닝은 많은 분야에서 다양한 응용 사례가 나올 것이다.
신경망 구조
신경망 구조는 비교적 단순하다. 신경망은 입력층, 은닉층, 출력층으로 구성된다.
신경망 구조(wikibooks)
신경망은 특정 Input 데이터 특징 패턴이 주어졌을 때, 학습된 특정 Output 데이터를 출력하게 된다. 신경망 학습은 Input 데이터와 Output 데이터(라벨. label) 간의 가중치를 통계적으로 조정하는 것이다. 신경망 구조에서 노드 간 연결 링크는 가중치를 포함한다.
v = W·x + b
여기서, x = 입력벡터
W = 가중치
b = bias값
계산된 v값을 출력값 y로 계산하는 것은 활성화함수(activation functions)이 한다. 활성화함수는 시그모이달, softmax 같은 함수가 있다.
y = φ(v)
여기서, φ = 활성함수
정답 label과 출력값y의 차이는 에러e로 정의한다.
e = d - y
여기서, d = 정답(라벨)
e = 오차
e = 오차
w = w + a·e·x ... 간략식
w = w
여기서, a = 학습률 (0 ~ 1)
φ' = φ 함수의 도함수 δ
학습규칙
학습규칙은 다음과 같은 것이 사용된다.
- Stochastic gradient descent(SGD. 경사하강법): 각 학습데이터 하나씩 가중치 갱신. 학습 성능이 무작위로 변하는 경향이 있음.
∆w = a·δ·x
w = w + ∆w
- 배치 방식(batch): 모든 학습 데이터 오차에 관한 가중치 갱신을 계산한 후 이들 평균값으로 가중치를 갱신하는 기법. 무작위 변화는 줄어드나, 학습 시간이 오래 걸림.
∆w = 1/n·∑∆w(k)
여기서, k는 k번째 학습 데이터- 미니 배치 방식(mini batch): 전체 학습 데이터 중 일부 데이터만 골라 배치 방식으로 학습.
시그모이달 함술수를 사용할 때 δ는 다음과 같다.
δ = φ(v) (1 - φ(v)) e
X = [0 0 1;
0 1 1;
1 0 1;
1 1 1;
];
D = [0
0
1
1
];
W = 2*rand(1, 3) - 1;
for epoch = 1:10000
W = DeltaSGD(W, X, D);
end
N = 4;
for k = 1:N
x = X(k, :)';
v = W * x;
y = Sigmoid(v)
end
function y = Sigmoid(x)
y = 1 / (1 + exp(-));
end
function W = DeltaSGD(W, X, D)
alpha = 0.9;
N = 4;
for k = 1:N
x = X(k, :)';
d = D(k);
v = W * x;
y = Sigmoid(v);
e = d - y;
delta = y. * (1-y). * e; % SGD
dW = alpha * delta * x';
W(1) = W(1) + dW(1);
W(2) = W(2) + dW(2);
W(3) = W(3) + dW(3);
end
end
역전파 알고리즘
역전파 알고리즘은 출력오차를 수식 왼쪽의 모든 은닉층 w를 조정해 간다. 다음은 matlab 코드 예이다.
function [W1, W2] = backprop(W1, W2, X, D)
alpha = 0.9;
N = 4;
for k = 1:N
x = X(k, :)';
d = D(k);
v1 = W1 * x;
y1 = Sigmoid(v1);
v = W2 * y1;
y = Sigmoid(v);
e = d - y;
delta = y. * (1-y). * e;
e1 = W2' * delta;
delta1 = y1. * (1-y). * e1;
dW1 = alpha * delta1 * x';
W1 = W1 + dW1;
dW2 = alpha * delta * y1';
W2 = W2 + dW2;
end
end
학습 규칙에 모멘텀(momentum)을 추가하면, 관성에 따라 일정 방향으로 가중치 갱신값이 커진다.
∆w = a·δ·x
m = ∆w + ß·m^
w = w + m
m^ = m
다음은 모멘텀을 추가한 코드이다.
function [W1, W2] = BackpropMnt(W1, W2, X, D)
alpha = 0.9;
beta = 0.9;
mmt1 = zeros(size(W1));
mmt2 = zeros(size(W2));
N = 4;
for k = 1:N
x = X(k, :)';
d = D(k);
v1 = W1 * x;
y1 = Sigmoid(v1);
v = W2 * y1;
y = Sigmoid(v);
e = d - y;
delta = y. * (1-y). * e;
e1 = W2' * delta;
delta1 = y1. * (1-y). * e1;
dW1 = alpha * delta1 * x';
mnt1 = dW1 + beta * mnt1;
W1 = W1 + mnt1;
dW2 = alpha * delta * y1';
mnt2 = dW2 + beta * mnt2;
W2 = W2 + mnt2;
end
end
비용함수
앞서 언급한 학습 규칙은 비용 함수에서 도출되었다. 신경망 오차가 크면, 비용 함수 값도 크다.
비용 함수(stats.stackexchange.com)
J = ∑1/n·(d - y)^2
Cross entropy함수는 Sum of squared error 보다 더 민감하게 반응해, 학습 성능이 더 좋다.
J = ∑{-d ln(y) - (1 - d)ln(1 - y)}
다음은 Cross entropy 비용함수 구현이다. 아래 경우, 활성함수가 시그모이드 함수일 경우, 델타와 출력 오차가 같다.
function [W1, W2] = BackpropCE(W1, W2, X, D)
alpha = 0.9;
N = 4;
for k = 1:N
x = X(k, :)';
d = D(k);
v1 = W1 * x;
y1 = Sigmoid(v1);
v = W2 * y1;
y = Sigmoid(v);
e = d - y;
delta = e;
e1 = W2' * delta;
delta1 = y1. * (1-y). * e1;
dW1 = alpha * delta1 * x';
W1 = W1 + dW1;
dW2 = alpha * delta * y1';
W2 = W2 + dW2;
end
end
다범주 분류
다범주 분류를 위해서는, 출력 노드 벡터를 one-hot 인코딩(1-of-N 인코딩)하는 것이 좋다.
예) 범주1 범주2 범주3
1 0 0
0 1 0
0 0 1
다범주 분류시에는 출력노드 활성함수로 소프트맥스(softmax) 함수를 사용하는 것이 일반적이다. 소프트맥스 함수는 자신 가중합 뿐 아니라, 다른 출력 노드들 가중합도 고려한다.
소프트맥스 함수는 각 출력 노드 값을 0 ~ 1로 제한할 뿐 아니라, 출력 노드 모든 합을 항상 1이 되게 한다. 시그모이드 함수의 경우, 자신 출력에만 관여하기 때문에 다음 출력도 가능하다.
예) 1
1
1
다음은 소프트맥스를 이용한 다범주분류의 예이다.alpha = 0.9;
N = 4;
for k = 1:N
x = X(k, :)';
d = D(k);
v1 = W1 * x;
y1 = Sigmoid(v1);
v = W2 * y1;
y = Sigmoid(v);
e = d - y;
delta = e;
e1 = W2' * delta;
delta1 = y1. * (1-y). * e1;
dW1 = alpha * delta1 * x';
W1 = W1 + dW1;
dW2 = alpha * delta * y1';
W2 = W2 + dW2;
end
end
다범주 분류
다범주 분류를 위해서는, 출력 노드 벡터를 one-hot 인코딩(1-of-N 인코딩)하는 것이 좋다.
예) 범주1 범주2 범주3
1 0 0
0 1 0
0 0 1
다범주 분류시에는 출력노드 활성함수로 소프트맥스(softmax) 함수를 사용하는 것이 일반적이다. 소프트맥스 함수는 자신 가중합 뿐 아니라, 다른 출력 노드들 가중합도 고려한다.
소프트맥스 함수는 각 출력 노드 값을 0 ~ 1로 제한할 뿐 아니라, 출력 노드 모든 합을 항상 1이 되게 한다. 시그모이드 함수의 경우, 자신 출력에만 관여하기 때문에 다음 출력도 가능하다.
예) 1
1
1
function [W1, W2] = MultiClass(W1, W2, X, D)
alpha = 0.9;
N = 5;
for k = 1:N
x = reshape(X(:, :, k), 25, 1); % 5x5 픽셀 1,2,3,4,5숫자 이미지 입력
d = D(k, :)';
v1 = W1 * x;
y1 = Sigmoid(v1);
v = W2 * y1;
y = Softmax(v);
e = d - y;
delta = e;
e1 = W2' * delta;
delta1 = y1. * (1-y). * e1;
dW1 = alpha * delta1 * x';
W1 = W1 + dW1;
dW2 = alpha * delta * y1';
W2 = W2 + dW2;
end
end
function y = Softmax(x)
ex = exp(x);
y = ex / sum(ex);
end
심층 신경망
역전파 알고리즘 문제는 다음과 같다.
- 그레디언트 소실(vanishing gradient): 앞쪽의 은직층까지 오차가 거의 전달되지 않는 현상
- 과적합(overfit): 은닉층을 늘릴 때,
- 많은 계산량
그레디언트 소실 문제는 활성함수를 ReLU(Rectified Linear Unit)을 적용해 해결할 수 있다.
φ(v) = x, x > 0
0, x <= 0
= max(0, x)
ReLU는 신경망 노드 출력이 1을 넘어갈 수 있다. 이를 통해, 그레디언트 소실 문제를 해결한다.
φ'(v) =1, x > 0
0, x <= 0
과적합은 입력값과 너무 적합하게 학습된 상황을 의미한다.
Under-fitting, generalized-fitting, over-fitting(The Shape of Data)
과적합 해결 책 중 하나는 드롭아웃(dropout) 기법이다. 드롭아웃은 신경망 전체를 학습하지 않고, 일부 노드만 무작위로 골라 학습한다. 보통, 드롭아웃 비율은 은닉층은 50%, 입력노드는 25% 수준이다.
다음은 ReLU 함수이다.
function y = ReLU(x)
y = max(0, x)
end
다음은 드롭아웃 함수이다.
function ym = Dropout(y, ratio)
[m, n] = size(y);
ym = zeros(m, n);
num = round(m * n * (1 - ratio));
idx = randperm(m * n, num);
ym(idx) = 1 / (1 - ratio);
end
컨벌루션 신경망
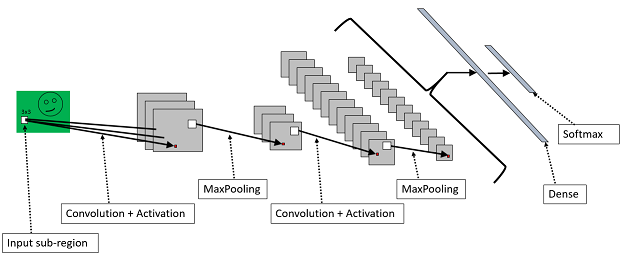
컨브넷는 학습 데이터의 특징을 추출하는 특징 추출기를 신경망 학습 과정에 포함시켜 일괄 처리한다. 특징 추출기 신경망의 가중치도 학습을 통해 결정된다.
컨브넷에 입력된 원본 이미지는 앞쪽의 특징 추출 신경망을 통과한다. 여기서 추출된 이미지 특징 맵(feature map)는 뒷 부분의 분류 신경망에 다시 입력된다. 분류 신경망은 이미지 특징을 기반으로 이미지 최종 범주를 분류한다.
Image - Conv - ReLU - Pool - Deep Neural Network (ReLU - Softmax) -> label
컨벌루션 레이어는 컨벌루션 연산을 통해 입력 이미지를 변환한다. 디지털 필터(컨벌루션 필터) 역할을 한다.
풀링(pooling) 레이어는 주위 픽셀을 묶어 하나의 대표 픽셀을 만든다. 이미지 차원을 축소하는 역할이다. 풀링은 입력 이미지에 인식 대상이 한 쪽으로 치우쳐있거나 돌아가 있는 것을 보상해 준다.
컨브넷는 학습 데이터의 특징을 추출하는 특징 추출기를 신경망 학습 과정에 포함시켜 일괄 처리한다. 특징 추출기 신경망의 가중치도 학습을 통해 결정된다.
컨브넷에 입력된 원본 이미지는 앞쪽의 특징 추출 신경망을 통과한다. 여기서 추출된 이미지 특징 맵(feature map)는 뒷 부분의 분류 신경망에 다시 입력된다. 분류 신경망은 이미지 특징을 기반으로 이미지 최종 범주를 분류한다.
Image - Conv - ReLU - Pool - Deep Neural Network (ReLU - Softmax) -> label
풀링(pooling) 레이어는 주위 픽셀을 묶어 하나의 대표 픽셀을 만든다. 이미지 차원을 축소하는 역할이다. 풀링은 입력 이미지에 인식 대상이 한 쪽으로 치우쳐있거나 돌아가 있는 것을 보상해 준다.
다음은 MNIST 이미지를 분류하는 CNN 코드이다.
function [W1, W5, Wo] = MnistConv(W1, W5, Wo, X, D)
alpha = 0.01;
beta = 0.95;
momentum1 = zeros(sizeof(W1);
momentum2 = zeros(sizeof(W5);
N = length(D);
bsize = 100; % 미니배치 학습 개수는 100개.
blist = 1:bsize:(N - bsize + 1); % 미니배치 방식 학습.
for batch = 1:length(blist)
dW1 = zeros(sizeof(W1));
dW5 = zeros(sizeof(W5));
dWo = zeros(sizeof(Wo));
begin = blist(batch);
for k = begin:begin + bsize - 1
x = X(:, :, k); % input, 28 x 28
y1 = Conv(x, W1); % conv, 20 x 20 x 20. W1을 받아, 필터를 구성함. 필터 20개.
y2 = ReLU(y1);
y3 = Pool(y2); % Pool, 10 x 10 x 20
y4 = reshape(y3, [], 1) % 2000
v5 = W5 * y4;
y5 = ReLU(v5);
v = Wo * y5;
y = Softmax(v);
% one-hot encoding
d = zeros(10, 1);
d(sub2ind(size(d), D(k), 1)) = 1;
% back propagation
e = d - y;
delta = e;
e5 = Wo' * delta; % hidden(ReLU) layer
delta5 = (y5 > 0) .* e5;
e4 = W5' * delta5;
e5 = reshape(e4, size(y3));
e2 = zeros(size(y2));
W3 = ones(size(y2)) / (2*2);
for c = 1:20
e2(:, :, c) = kron(e3(:, :, c), ones([2 2])) .* W3(:, :, c);
end
delta2 = (y2 > 0) .* e2; % ReLU layer
delta1_x = zeros(size(W1)); % Conv layer
for c = 1:20
delta1_x(:, :, c) = conv2(:, :), rot90(delta2(:, :, c), 2), 'valid');
end
% update weights
dW1 = dW1 / bsize;
dW5 = dW5 / bsize;
dWo = dWo / bsize;
momentum1 = alpha * dW1 + beta * momentum1;
W1 = W1 + momentum1;
momentum5 = alpha * dW5 + beta * momentum5;
W5 = W5 + momentum5;
end
alpha = 0.01;
beta = 0.95;
momentum1 = zeros(sizeof(W1);
momentum2 = zeros(sizeof(W5);
momentum3 = zeros(sizeof(Wo);
bsize = 100; % 미니배치 학습 개수는 100개.
blist = 1:bsize:(N - bsize + 1); % 미니배치 방식 학습.
for batch = 1:length(blist)
dW1 = zeros(sizeof(W1));
dW5 = zeros(sizeof(W5));
dWo = zeros(sizeof(Wo));
begin = blist(batch);
for k = begin:begin + bsize - 1
x = X(:, :, k); % input, 28 x 28
y1 = Conv(x, W1); % conv, 20 x 20 x 20. W1을 받아, 필터를 구성함. 필터 20개.
y2 = ReLU(y1);
y3 = Pool(y2); % Pool, 10 x 10 x 20
y4 = reshape(y3, [], 1) % 2000
v5 = W5 * y4;
y5 = ReLU(v5);
v = Wo * y5;
y = Softmax(v);
% one-hot encoding
d = zeros(10, 1);
d(sub2ind(size(d), D(k), 1)) = 1;
% back propagation
e = d - y;
delta = e;
e5 = Wo' * delta; % hidden(ReLU) layer
delta5 = (y5 > 0) .* e5;
e4 = W5' * delta5;
e5 = reshape(e4, size(y3));
e2 = zeros(size(y2));
W3 = ones(size(y2)) / (2*2);
for c = 1:20
e2(:, :, c) = kron(e3(:, :, c), ones([2 2])) .* W3(:, :, c);
end
delta2 = (y2 > 0) .* e2; % ReLU layer
delta1_x = zeros(size(W1)); % Conv layer
for c = 1:20
delta1_x(:, :, c) = conv2(:, :), rot90(delta2(:, :, c), 2), 'valid');
end
dW1 = dW1 + delta1_x;
dW5 = dW5 + delta5 * y4';
dWo = dWo + delta * y5';
end
% update weights
dW1 = dW1 / bsize;
dW5 = dW5 / bsize;
dWo = dWo / bsize;
momentum1 = alpha * dW1 + beta * momentum1;
W1 = W1 + momentum1;
momentum5 = alpha * dW5 + beta * momentum5;
W5 = W5 + momentum5;
momentumo = alpha * dWo + beta * momentumo;
Wo = Wo + momentumo;
endWo = Wo + momentumo;
end
RNN과 LSTM
이 모델은 순서가 있는 시계열 데이터의 일부를 학습데이터와 라벨링데이터로 활용해 시계열 데이터 자체에 포함된 패턴을 학습한다. 이를 통해, 소설쓰기, 작곡 작사, 주가 예측 등이 가능하다.
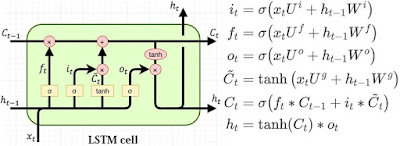
LSTM 모델
LSTM 단위
U-Net과 인코딩-디코딩
U-Net은 인코딩과 디코딩(encoding - decoding)이 반대로 붙어 있는 모양으로 정의된 딥러닝 모델이다. ResNet과 같이 skip connection을 지원하므로, 입력 데이터에서 특징을 추출하며 일반화될 때 발생하는 데이터 크기가 작아지는 문제를 해결한다. 그러므로, 데이터 세그먼테이션에 주로 많이 사용된다.
트랜스포머와 어텐션
트랜스포머(transformer)와 어텐션(attention)는 데이터에서 위치를 인코딩해, 공간 데이터 특징을 캡쳐할 수 있도록 인코딩을 설계하고, 데이터 간의 관계에 대한 특징을 학습함으로써, 이와 관련된 모든 딥러닝 모델에 적용될 수 있도록 개발되었다. 다국어 번억, 챗봇, 문서 텍스트 마이닝 및 특징 분류, 이미지 세그먼테이션 등 다양한 곳에 사용된다.
GCN과 GDL
GCN(Graph Convolutional Networks. GNN)과 GDL (Geometric Deep Learning)은 다음 그림과 같이, 재료를 구성하는 화학 분자 분석, 탐지 및 설계, 영상 컨텍스트 해석 및 생성, 다차원 포인트 클라우드 세그먼테이션 등 다양한 영역에서 사용된다. 자세한 내용은 여기를 참고한다.
최근 나오고 있는 신경망들은 대부분 앞의 개념에 기반한다. 신경망은 학습모델을 만드는 통계적 기법이다. 앞서 언급된 모델들은 Keras, PyTorch로 구현되어, YOLO, OpenAI, Bert 와 같은 이름으로 공개되고 있다. 딥러닝은 좀 더 범용적인 문제를 해결할 수 있도록 발전될 것이다.
레퍼런스
1. 병렬처리 – First Contact with TensorFlow
2. Deep Learning을 위해 어떤 GPU를 써야 할까?
3. 김성필, 딥러닝 첫걸음
4. wikibooks, Artificial Neural Networks/Print Version
5. Google, 텐서플로우 메뉴얼
6. YOLO: real-time object detection (paper)
7. ConvNetJS
8. carpedm20.github.io/faces