이 글은 ICP(Iterative Closest Point) 알고리즘 및 실행방법을 설명한다.
ICP는 카메라, 라이다 등을 통해 생성된 3차원 점군을 정합해 실내외 지도를 만드는 데 핵심적으로 활용되는 알고리즘이다. 대부분의 SLAM(Simultaneous localization and mapping)알고리즘은 ICP를 응용 목적에 따라 수정해 개발한 것이다. 그래서, 수학적 계산 모델은 ICP, SLAM 모두 유사하다.
ICP는 한 대상물에 대해 다른 지점에서 스캔된 두개의 포인트 클라우드가 있을 경우, 이 두개의 데이터를 퍼즐처럼 합쳐, 정합(registration)하는 알고리즘이다. 반복적으로 가장 근접된 점들을 퍼즐처럼 맞춰주기 때문에 Iterative Closest Point 이라 한다.
이 글은 ICP개념, 알고리즘 및 간단한 구현 방법을 살펴보고, SLAM과의 차이점을 알아본다. 이 글을 통해, SLAM알고리즘을 좀 더 깊게 이해할 수 있고, 각자 응용에 따른 로보틱스 기반 실내외 지도 생성 알고리즘 개발 등에 도움이 될 것이다.
ICP는 카메라, 라이다 등을 통해 생성된 점군을 정합해 실내외 지도를 만드는 데 핵심적으로 활용되는 알고리즘이다. 대부분의 SLAM(Simultaneous localization and mapping)알고리즘은 ICP를 응용 상황에 따라 수정해 개발한 것이다. 그래서, 수학적 계산 모델은 ICP, SLAM 모두 유사하다.
SLAM은 실시간 정합을 위해, 공간인덱싱 등 속도를 많이 고려하였고, 특징점 추출도 최대한 계산량을 줄일 수 있도록 처리되어 있다.
ICP는 로컬라이제이션 및 매핑(Mapping) 기술로 자율이동 시스템의 탐색 이동 작업을 수행하기 위한 핵심기술이다. ICP는 로봇에서 LiDAR 스캔 매칭에 널리 적용된다. 스캔된 점군 사이에 가장 가까운 점을 찾는 ICP알고리즘은 많은 비용이 필요하다. 특히 대규모 포인트 클라우드 데이터를 처리할 때, 실시간 요구 사항을 충족하기는 어렵다.
카메라 기반 사진측량이나 LiDAR는 스캔할 때 많은 수의 렌드마크(Landmark. 특징점) 지점을 생성하지만, 이러한 지점 중 상당수는 쓸모가 없으며, 후속 처리의 부담을 증가시킨다. 이 문제는 다수 렌드마크에서 노이즈 필터링로 해결될 수 있다. 예를 들어, 렌드마크에서 그라운드(Ground) 포인트를 제거한다. 이 단계 후에 표준적인 알고리즘인 Point to Point ICP가 적용되어, 연속된 스캔 점군 간의 6자유도 변환 행렬을 계산한다. 또한, 스캔 환경에서 폐쇄 루프(Close Loop)가 감지되면 전역 적으로 6D 그래프 최적화 알고리즘을 적용할 수 있다.
포인트 클라우드 정합(Registration)은 지도 매핑을 위한 로봇 시스템의 핵심이다. 위치가 다른 두 개의 인접한 포인트 클라우드 스캔이 주어지면 목표는 이 두 스캔을 가장 잘 정렬하는 변환행렬을 찾는 것이다.
일반적인 점 기반 방법은 선택된 가장 가까운 점에 따라 두 점군 사이의 변환 적용 시 거리 함수를 최소화한다. 이 방법은 정합 소프트웨어에서 가장 널리 사용되는 방법이다. 이외에, 포인트 클라우드에서 일부 하위 수준 속성을 추출하여, 스캔 매칭을 수행할 수도 있다. 예를 들어, 법선, 강도, 평면 표면, 모서리 및 사용자 정의 설명자와 같은 의미론적 정보를 사용한다. 이를 특징점이라 말한다. 이 특징점을 사용하여 스캔 사이의 점 대응 관계를 찾는다. 예를 들어, LOAM(Lidar Odometry and Mapping)은 가장자리 및 평면 특징을 추출하여 고정밀 맵을 생성한다. 그러나 많은 특징점은 특정 환경 조건에서 적용하도록 설계되었다. 특징점 기반 방법은 고속도로와 같이 기하학적 정보가 낮고 변화가 별로 없는 환경에서 낮은 품질을 갖는다.
또 다른 유형의 알고리즘은 분포 기반 방법이다. 정규 분포 변환(NDT)은 점군을 가우스 확률 분포 집합으로 나타낸다. 점에 대해 직접 계산하는 대신, 이 방법은 점-분포 또는 분포-분포 대응을 반복적으로 계산하고, 각 반복 단계에서 거리 함수를 최소화한다.
앞서 언급한 누적 오류를 제한할 수 있는 또 다른 방법은 포인트 기반 스캔 매칭 알고리즘과 특징 기반 매핑을 결합하는 것이다.
SLAM(동시 현지화 및 매핑)은 프런트엔드(Frontend)와 백엔드(Backend)의 두 부분으로 구성된다. 프런트엔드에는 데이터 연결 및 센서 자세 초기화가 포함된다. 백엔드에서는 필터링 방법, 포즈 그래프 최적화 방법이 사용된다. 그래프 기반 최적화는 SLAM 분야에서 가장 널리 사용되는 기술이다.
관련 기술들
LiDAR로 얻은 포인트 클라우드에는 많은 그라운드 포인트가 포함되어 있다. 따라서 포인트 클라우드 전처리 단계에서 그라운드 포인트 제거가 중요한다. 일반적인 접근 방식은 Bounding Box Filter이다. 이를 사용하여 직사각형 경계 영역에서 점을 제외할 수 있다. 또 다른 방법은 법선과 기울기를 사용하여 로컬 특징을 계산한 다음, 영역 성장(Region grown)알고리즘을 수행하여 그라운드를 추출했다. 포인트 클라우드를 투영한 그라운드 포인트를 추출할 수도 있다. 투영을 통해 3차원 점군은 2차원 이미지로 생성된다. 이 경우 계산량은 크게 줄어든다.
머신 러닝을 기반으로 한 포인트 클라우드 세그먼테이션도 좋은 접근이다. CNN(Convolutional Neural Network)을 이용해, 그라운드 지점과 아닌 지점을 분할할 수 있다. 하지만, 이러한 지도 학습 방법은 모델을 훈련하기 위해 미리 레이블이 지정된 데이터 세트가 필요한다.
백엔드에서는 필터 기반 방법, 포즈 그래프 최적화 방법이 사용된다. 이 프로세스는 전역적으로 일관된 매핑을 얻는 것을 목표로 한다. 확장 칼만 필터와 같은 필터 기반 방법에는 널리 사용된다.
포즈 그래프 최적화 방법은 SLAM에서 더 큰 이점이 있다. 예를 들어, ICP를 사용하여 수렴될 때까지 모든 스캔을 정합하는 6D SLAM 방법이 있다. 폐쇄 루프가 감지되면, 전역 완화를 위한 GraphSLAM이 사용된다. LEGO-LOAM은 먼저 포인트 클라우드를 2D 이미지로 투영한다. 그런 다음 포인트 클라우드는 지상 및 비지상 포인트로 세분화된다. 특징점 추출 및 매칭 오차 함수는 6자유도 포즈를 추정하는 데 사용된다. 보다 정확한 결과를 얻기 위해 포즈 그래프 SLAM를 통합했다. LOAM은 실시간 작업을 충족함과 동시에 높은 포즈 추정 정확도를 달성한다. 그러나 특징점 기반 방법은 고속도로와 같이 기하학적 정보가 낮은 환경에서 부정확한 정합으로 이어질 수 있다.
ICP 알고리즘
ICP는 선택된 가장 가까운 점에 따라 두 점군 사이의 변환을 계산하기 위해, 거리 함수를 최소화한다.
E(R,t)=∑i=1Nm∑j=1Nd∥si−(Rdj+t)∥2
Point-to-plane ICP알고리즘은 소스 포인트와 타겟 포인트의 접평면 사이의 거리 제곱의 합을 최소화할 수도 있다. 다만, 이 경우, 법선을 계산하는 비용이 실시간 지도 생성에 맞지 않을 수 있다.
Topt=argminT∑i=1N((Tsi−di)ni)2
여기는 파이썬으로 구현된 점 대 점 ICP 알고리즘
구현코드를 분석해 설명한다. 참고로, 이 코드는 현재 아마존 로보틱스기술 개발 시니어 매니저인
Clay Flannigan이 구현한 것이다. ICP 구현 코드 중 가장 직관적으로 되어 있어 이를 활용해 설명한다.
import numpy as np
from sklearn.neighbors import NearestNeighbors
def icp(A, B, init_pose=None, max_iterations=20, tolerance=0.001):
'''
주어짐 점군 A, B에 대해 정합 행렬을 계산해 리턴함.
Input:
A: numpy 형태 Nxm 행렬. 소스(Src) mD points
B: numpy 형태 Nxm 행렬. 대상(Dst) mD points
init_pose: (m+1)x(m+1) 동차좌표계(homogeneous) 변환행렬
max_iterations: 알고리즘 계산 중지 탈출 횟수
tolerance: 수렴 허용치 기준
Output:
T: 최종 동차좌표계 변환 행렬. maps A on to B
distances: 가장 가까운 이웃점 간 유클리드 오차 거리
i: 수렴 반복 횟수
'''
assert A.shape == B.shape
# 차원 획득
m = A.shape[1]
# 동차 좌표계 행렬을 만들고, 점군 자료를 추가
src = np.ones((m+1, A.shape[0]))
dst = np.ones((m+1, B.shape[0]))
src[:m,:] = np.copy(A.T)
dst[:m,:] = np.copy(B.T)
# src 점군에 초기 자세 적용
if init_pose is not None:
src = np.dot(init_pose, src)
prev_error = 0
for i in range(max_iterations): # 정합될때까지 반복 계산
# 소스와 목적 점군 간에 가장 근처 이웃점 탐색. 계산량이 많음.
distances, indices = nearest_neighbor(src[:m,:].T, dst[:m,:].T)
# 소스 점군에서 대상 점군으로 정합 시 필요한 변환행렬 계산
T,_,_ = best_fit_transform(src[:m,:].T, dst[:m,indices].T)
# 소스 점군에 변환행렬 적용해 좌표 갱신
src = np.dot(T, src)
# 에러값 계산
mean_error = np.mean(distances)
if np.abs(prev_error - mean_error) < tolerance: # 허용치보다 에러 작으면 탈출
break
prev_error = mean_error
# 변환행렬 계산
T,_,_ = best_fit_transform(A, src[:m,:].T)
return T, distances, i
def nearest_neighbor(src, dst):
'''
소스와 목적 점군에 대한 가장 이웃한 점 계산
Input:
src: Nxm array of points
dst: Nxm array of points
Output:
distances: 가장 가까운 이웃점간 유클리드 거리
indices: 목적 점군에 대한 가장 가까웃 이웃점의 인덱스들
'''
assert src.shape == dst.shape
neigh = NearestNeighbors(n_neighbors=1)
neigh.fit(dst)
distances, indices = neigh.kneighbors(src, return_distance=True)
return distances.ravel(), indices.ravel()
def best_fit_transform(A, B):
'''
m 공간 차원에서 점군 A에서 B로 맵핑을 위한 최소자승법 변환행렬 계산
Input:
A: Nxm numpy array of corresponding points
B: Nxm numpy array of corresponding points
Returns:
T: (m+1)x(m+1) 동차좌표 변환행렬. maps A on to B
R: mxm rotation matrix
t: mx1 translation vector
'''
assert A.shape == B.shape
# 차원 얻기
m = A.shape[1]
# 각 점군 중심점 및 중심 편차 계산
centroid_A = np.mean(A, axis=0)
centroid_B = np.mean(B, axis=0)
AA = A - centroid_A # A행렬 편차
BB = B - centroid_B # B행렬 편차
H = np.dot(AA.T, BB) # 분산
U, S, Vt = np.linalg.svd(H) # SVD 계산 R = np.dot(Vt.T, U.T) # 회전 행렬
# 반사된 경우 행렬 계산
if np.linalg.det(R) < 0:
Vt[m-1,:] *= -1
R = np.dot(Vt.T, U.T)
# 이동 행렬 계산
t = centroid_B.T - np.dot(R, centroid_A.T) #
# 동차 변환행렬 계산
T = np.identity(m+1)
T[:m, :m] = R # 회전 행렬
T[:m, m] = t # 이동 행렬
return T, R, t
여기서, SVD(Singular Value Decomposition. 특이값분해)는 주어진 점군에서 차원을 축소해, 변환행렬에 필요한 요소를 구한다.
여기서, 분해하려는 행렬 M은 m x n 실수 행렬이다.
- U: m x m 직교 행렬. 회전 변환
 : m x n 대각 행렬. 스케일 변환
: m x n 대각 행렬. 스케일 변환- VT: n x n 직교 행렬. 회전 변환
import numpy as np
import time
import icp
# Constants
N = 10 # 데이터셋 크기
num_tests = 10 # 반복 테스트 계산 횟수
dim = 3 # 데이터 포인트 차원
noise_sigma = .01 # 노이즈 표준 편차
translation = .1 # 테스트셋 최대 이동 거리
rotation = .1 # 테스트셋 최대 회전 각
def test_icp():
# 임의 데이터셋 생성
A = np.random.rand(N, dim)
total_time = 0
for i in range(num_tests):
B = np.copy(A)
# 테스트 데이터셋 이동
t = np.random.rand(dim)*translation
B += t
# 회전
R = rotation_matrix(np.random.rand(dim), np.random.rand() * rotation)
B = np.dot(R, B.T).T
# 노이즈 추가
B += np.random.randn(N, dim) * noise_sigma
# 위치 섞음
np.random.shuffle(B)
# ICP 알고리즘 실행
start = time.time()
T, distances, iterations = icp.icp(B, A, tolerance=0.000001)
total_time += time.time() - start
# 동차좌표 생성
C = np.ones((N, 4))
C[:,0:3] = np.copy(B)
# 변환행렬 적용
C = np.dot(T, C.T).T
print('distance: {:.3}'.format(np.mean(distances)))
assert np.mean(distances) < 6*noise_sigma # 평균 에러
assert np.allclose(T[0:3,0:3].T, R, atol=6*noise_sigma) # T and R should be inverses
assert np.allclose(-T[0:3,3], t, atol=6*noise_sigma) # T and t should be inverses
print('icp time: {:.3}'.format(total_time/num_tests))
return
실행 결과는 다음과 같다. 잘 정합되는 것을 확인할 수 있다.
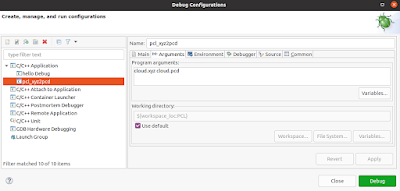
점군 간 정합 알고리즘 코드를 디버깅하면, 다음과 같이 SVD를 계산해, 변환행렬을 계산하는 것을 확인할 수 있다. 이 변환행렬을 정합 대상이 되는 점군에 적용해가면서, 정합 퍼즐을 맞춰나간다.
앞서 설명한 알고리즘이 점군 정합에 어떤식으로 동작하는 지 확인해 보기 위해, 각 수렴단계를 파일로 저장하여 동작을 가시화해본다. 다음과 같이 test.py 모듈에 사인 모양 점군을 생성하고, ICP()함수안에 각 정합 단계별로 파일을 저장하도록 코드를 추가한다.
icp._index = 0
def test_icp():
# Generate a random dataset
# A = np.random.rand(N, dim)
A = np.zeros((N, dim))
x = np.arange(0, 3 * np.pi, 3 * np.pi / N) # create x array of angels from range 0 to 3*3.14
y = np.sin(x)
z = np.sin(x)
for i in range(N):
A[i][0] = x[i]
A[i][1] = y[i]
A[i][2] = z[i]
...
_index = 0
def icp(A, B, init_pose=None, max_iterations=20, tolerance=0.001):
...
for i in range(max_iterations):
# find the nearest neighbors between the current source and destination points
distances, indices = nearest_neighbor(src[:m,:].T, dst[:m,:].T)
_index = _index + 1
fname = "point_" + str(_index) + ".xyz"
f = open(fname, "a")
for data in src.T:
point = np.array2string(data, separator=',')
point = point.replace('[', '')
point = point.replace(']', '')
f.write(point)
f.write('\n')
f.close()
...
test.py 안의 전역변수를 아래와 같이 수정해, 정합할 대상 점군과 원본 점군과의 차이를 크게 한다.
noise_sigma = 0.1 # standard deviation error to be added
translation = 1.0 # max translation of the test set
rotation = 1.0 # max rotation (radians) of the test set
test.py를 실행해, 저장된 xyz 파일을
CloudCompare로 확인해 보면, 다음과 같이 녹색 점군이 흰색 점군으로 잘 정합되는 것을 확인할 수 있다.
SVD는 전역적인 최적화이므로, 지역적인 매칭은 오차가 있다. 예를 들어, 일부만 매칭하는 경우, 다음과 같이 오차가 크다는 것을 알 수 있다.
SVD기반 정합 결과(흰색 = 목표, 녹색 = 초기 점군, 적색 = 정합된 점군)
PCL ICP
PCL(Point Cloud Library)을 설치한 후, 구현된 ICP를 실행해 본다. 다음과 같이 스캔한 두개의 점군 데이터를 준비하여, 하나를 회전 이동 변환해 본다.
../pcl_transform_point_cloud -trans 5,5,5 -quat 0.5,0,0,1 s3.pcd s3_tr2.pcd
다음과 같이 두 데이터를 정합한다. 정합 시간은 1분 정도 소요되었다.
../pcl_icp -d 10 s1.pcd s3_tr1.pcd
제대로 정합된 결과를 확인할 수 있다.
좀 더 자세히 설명하면, 대학교 건물을 각각 다른 장면에서 스캔한 두개의 데이터셋이 있다. 그 중 하나를 x, y, z각각 5미터만큼 이동하고, 쿼터니언 각도로 0.5 회전시켰다.
PCL에 구현된 ICP 주요 단계는 다음과 같다.
icp->setMaximumIterations (iter);
icp->setMaxCorrespondenceDistance (dist);
icp->setRANSACOutlierRejectionThreshold (rans);
iicp.setRegistration(icp);
pcd = LoadPCDFile();
iicp.registerCloud(pcd);
전통적인 ICP 알고리즘 한계
ICP 모든 점군에 대해 이를 계산하므로 계산속도 문제는 여전히 존재한다. 실시간 처리가 불가능하다. 만약, 무인자율로봇이 주변을 탐색해 경계나 장애물을 제외하고 특정 경로로 움직이고자 할 때는 ICP방식으로는 실시간 동작을 지원할 수가 없다(예. 주변공간의 특정한 모양을 가진 지점을 방문하거나, 공간 전체를 고르게 탐색하거나, 공간을 사람이 지시한 방향의 경계까지 최단경로로 목적지까지 가도록 하거나 등.. 사람이라면 자연스럽게 하는 공간탐색 후 행동전략은 모두 실시간임). 그러므로, 다음과 같은 솔류션으로 문제를 개선한다.
- 정합 대상이 되는 점군에서 특징점만 얻어 계산하면 속도와 정확성이 높아진다.
- 변환행렬 계산 속도를 개선한다.
1은 공간인덱싱 기술인 공간분할 a)을 적용하고, 특징점 b)과 관련없는 점군은 필터링 c)한다.
2는 1을 적용하고, 각 격자별로 통계적 특징 d)을 얻어, 정합 변환행렬 해 e) 계산량을 줄일 수 있다. 예를 들어, NDT(Normal Distribution Transform)을 사용해 계량산을 줄일 수 있다.
각 단계별 사용되는 알고리즘 예시는 다음과 같다.
Octree 기반 공간분할 예시
SLAM 알고리즘 구현 예시
주어진 3D 포인트 클라우드 계산량을 줄이기 위해, 보통, 공간인덱싱 구조를 사용한다. 예를 들어, 옥트리(Octree) 기반 데이터 구조를 적용한다. 이를 통해, 점군 검색 등의 속도를 획기적으로 개선할 수 있다. 이제, 점군 간 매칭될 특징점 대상수를 줄여야 실시간 스캔 데이터 정합이 가능하다. 예를 들어, 이미지 기반 그라운드 포인트 제거 방법을 적용한다. 이후, 표준적인 점 대 점 ICP 알고리즘이 적용되어, 연속된 스캔 점군 간의 6자유도 변환을 계산한다. 만약, 스캔 환경에서 폐쇄 루프가 감지되면 전역 이완을 위한 6D 그래프 최적화 알고리즘이 사용된다.
ICP 기반 실시간 맵 생성(Xuyou Li, 2020)
LiDAR의 고해상도는 스캔할 때 대규모 데이터를 수집한다. 예를 들어, Velodyne HDL-64E는 초당 180만 점군을 생성할 수 있다. 방대한 양의 3D 데이터 포인트를 효율적으로 처리하기 위해서는 포인트 클라우드 저장 및 축소가 중요한 단계이다. Octree는 3차원 포인트 클라우드의 효율적인 저장, 압축 및 검색을 가능하게 하는 3차원 공간 인덱싱 기술이다.
그라운드 점 제거 및 분할 알고리즘은 2D 이미지를 기반으로 처리한다. 투영된 각 3D 좌표점은 고유한 픽셀로 표시된다. 그라운드 점군은 다른 점군보다 밀도, 법선각도 등의 차이가 있다. 이를 이용해 세그먼테이션 후 제거를 한다. 이후, 처리된 점군에 대한 일부 노이즈 및 이상치 포인트도 필터링된다.
필터링된 점군에서 표준적인 점대점 ICP 알고리즘을 적용하여, 연속 스캔 간의 6자유도 변환을 계산한다.
ICP는 인접한 두 스캔 사이의 포즈를 계산한 다음, 지속적으로 업데이트하여, 궤적을 얻는다. 그러나 포즈 추정은 장기간 또는 대규모 스캔 장면에서 오차가 누적되는 문제가 있다. 이 문제를 해결하기 위해 폐쇄 루프가 감지되면, ICP의 포즈 추정 결과가 6D SLAM에 전역적으로 조정되도록 한다. 포즈 그래프 최적화 방법은 마할라노비스 거리(Mahalanobis distance)를 사용하여 모든 포즈의 전역 오류를 최소화한다. 마할라노비스 거리는 포즈 데이터의 평균과의 거리가 표준편차의 몇 배인지를 계산한다. 구체적인 공식은 다음과 같다.
이 글을 통해, ICP, SLAM 알고리즘 동작 방식을 알아보았다. ICP와 SLAM코드의 동작 방식을 이해하면, 왜 스캔 장면이 급격하게 변하거나 변화가 없는 장면 데이터를 정합할 때는 에러가 많아지는 지 이해할 수 있을 것이다. 그럼에도, 스캔 장비 성능이 좋아지고, 관련 데이터도 점차 많아질 것이므로, 이런 기술은 앞으로도 크게 중요해지리라 생각한다.











 : m x n 대각 행렬. 스케일 변환
: m x n 대각 행렬. 스케일 변환















