많은 유용한 딥러닝 기술이 릴리즈되고 있다. 그 중에 GCN(Graph Convolutional Networks. GNN)과 GDL (Geometric Deep Learning)에 대해 이야기를 나누어 보자.
GCN은 다음 그림과 같이, 재료를 구성하는 화학 분자 분석, 탐지 및 설계, 영상 컨텍스트 해석 및 생성, 다차원 포인트 클라우드 세그먼테이션 등 다양한 영역에서 사용된다.
GCN based application (Learning 3D Semantic Scene Graphs from 3D Indoor Reconstructions. link)
Example. Machine Learning for Scent: Learning Generalizable Perceptual Representations of Small Molecules (link)
Deep learning (Michael Bronstein, 2021, Geometric foundations of Deep Learning)
GNN과 MLP의 관계: GNN은 왜 필요한가?
그래프 신경망(GNN)의 작동 원리를 처음 접하면, 이는 다층 퍼셉트론(MLP)의 구조를 변형하여 노드 간의 관계 정보를 주입하는 방식이 아닌가 하는 의문이 생길 수 있다. 이 기술 노트는 이러한 관점에서 출발하여, 왜 단순 MLP만으로는 그래프 구조를 학습하기에 부족한지, 그리고 GNN이 어떤 방식으로 이 한계를 극복하며 MLP와 근본적으로 어떤 구조적 차이를 갖는지 분석하는 것을 목표로 한다. 결론적으로, GNN은 주변 노드의 정보를 점진적으로 취합한다는 점에서 MLP의 아이디어를 확장한 것이 맞지만, 그래프의 특성을 처리하기 위한 핵심적인 구조적 장치를 갖춘, 근본적으로 다른 아키텍처이다.
그래프 데이터를 일반적인 MLP 모델로 학습시킨다고 가정해 보자. 이 접근법은 각 노드를 독립된 데이터 샘플로 간주한다.
- 입력: [노드 개수, 특징 차원] 크기의 노드 특징 행렬
- 학습: MLP는 각 노드의 특징 벡터 x_A를 입력받아, 해당 노드의 레이블 y_A를 예측하는 함수를 학습한다.
- 문제점: 이 과정에서 그래프의 가장 중요한 정보인 연결 구조(엣지 정보)가 완전히 무시된다.
GNN은 "주변 노드의 특징을 점진적으로 통합하며 학습하는 MLP의 확장된 구조"로 이해할 수 있다. 이 과정은 '홉(hop)'이라는 개념으로 설명되며, GNN 레이어의 깊이와 직접적으로 연관된다.
1-홉(1-hop) 탐색: 첫 번째 GNN 레이어
하나의 GNN 레이어는 다음과 같은 3단계 연산을 통해 1차 이웃의 정보를 취합한다.
정보 수집 (Aggregation): 특정 노드 A를 기준으로, 엣지로 직접 연결된 모든 이웃 노드(B, C, D)의 특징 벡터를 수집한다.
정보 취합: 수집된 이웃 노드들의 특징 벡터를 가중 평균, 합산(Sum), 평균(Mean) 등의 함수를 통해 하나의 벡터로 요약한다. 이를 통해 이웃 정보 요약 벡터 h_N(A)가 생성된다.
정보 갱신 (Update): 노드 A의 자기 자신 특징 벡터 x_A와 이웃 정보 요약 벡터 h_N(A)를 결합한 후, 신경망(예: MLP 레이어)에 통과시켜 노드 A의 **새로운 특징 벡터 x'_A**를 생성한다.
이 과정을 거친 x'_A는 자신과 1차 이웃의 정보를 모두 포함하는, 더 풍부한 문맥을 가진 벡터가 된다. 이것이 바로 1홉 탐색의 결과물이다.
k-홉(k-hop) 탐색: GNN 레이어의 적층
GNN 레이어를 k개 쌓는 것은 k-홉 반경까지의 이웃 정보를 점진적으로 통합하는 과정이다.
2차 GNN 레이어: 첫 번째 레이어에서 갱신된 x' 벡터들을 입력으로 받는다. 노드 A는 이웃 B, C, D로부터 갱신된 특징 x'_B, x'_C, x'_D를 수집한다.정보의 전파: x'_B에는 이미 B의 1차 이웃 정보가 담겨있다. 따라서 A가 이 정보를 취합하면, A의 2차 이웃(2-hop neighbor) 정보까지 간접적으로 전달받게 된다.
결론적으로, k개의 GNN 레이어를 통과한 노드의 최종 특징 벡터는 해당 노드로부터 k 거리 이내에 있는 모든 노드의 정보를 종합적으로 반영하게 된다.
GNN이 단순한 MLP의 변형을 넘어 독자적인 아키텍처로 인정받는 이유는 그래프 데이터를 처리하기 위한 다음과 같은 핵심 특징 때문이다.
- 파라미터 공유 (Parameter Sharing): 하나의 GNN 레이어 내에서 정보 갱신에 사용되는 신경망(가중치 행렬)은 그래프 내의 모든 노드에 동일하게 적용된다. 이는 CNN의 필터처럼, 노드의 위치가 아닌 관계의 패턴을 학습하게 하여 모델의 효율성과 일반화 성능을 극대화한다.
- 순서 불변성 (Permutation Invariance): 노드의 이웃들은 순서가 없다. GNN의 취합 함수(평균, 합산 등)는 이웃 노드들의 정보가 어떤 순서로 입력되더라도 항상 동일한 결과를 출력하도록 설계되어, 그래프의 본질적인 특성을 보존한다.
- 가변적 이웃 수 처리: 노드마다 연결된 이웃의 수는 모두 다르다. GNN의 취합 함수는 입력받는 이웃 벡터의 개수에 상관없이 항상 고정된 크기의 결과 벡터를 출력하므로, 불규칙한 구조의 그래프에 자연스럽게 적용될 수 있다.
GCN의 각 레이어는 노드가 자신의 직접적인 이웃 노드들의 특징 정보를 받아와 자신의 기존 특징과 결합하는 '정보 혼합' 단계로 정의된다. 노드의 연결성(Degree), 즉 이웃 노드의 수는 정보 혼합의 다양성에 직접적인 영향을 미친다.
GCN은 이를 해결하기 위해 정규화(Normalization) 메커니즘을 내장하고 있다. 이는 연결이 많은 노드의 영향력은 줄이고 연결이 적은 노드의 영향력은 키워 정보 흐름의 균형을 맞추는 역할을 한다. 이 정규화 기법 덕분에 허브 노드는 다양한 정보를 효율적으로 취합하면서도 자신의 고유 정보를 완전히 잃지 않아, 전체 네트워크가 안정적으로 학습을 진행할 수 있게 된다.
GCN의 컨볼루션 연산은 이미지 처리에 사용되는 CNN(Convolutional Neural Network)의 컨볼루션과 개념적으로 유사하지만, 처리하는 데이터의 구조에서 근본적인 차이가 있다.
요약하자면, CNN은 고정된 이웃 관계를 갖는 정형 데이터에 최적화되어 있고, GCN은 이웃의 수와 관계가 모두 다른 비정형 그래프 데이터의 특징을 추출하는 데 특화되어 있다.
GCN에서 홉(Hop)은 정보가 그래프를 따라 얼마나 멀리 퍼져나가는지를 의미한다. 층을 깊게 쌓을수록 노드는 더 넓은 범위의 그래프 구조를 인식하게 된다.
GCN은 반복적인 정보 혼합과 정규화 과정을 통해 그래프 내 노드들의 관계성과 구조적 맥락을 학습한다. 이는 고정된 격자 구조를 가정하는 CNN과 달리, 불규칙하고 복잡한 관계를 갖는 데이터에서 패턴을 발견하는 데 매우 효과적인 방법론이다. GCN의 홉(레이어) 수는 노드가 얼마나 넓은 범위의 정보를 받아들일지를 결정하는 핵심 요소로 작용한다.
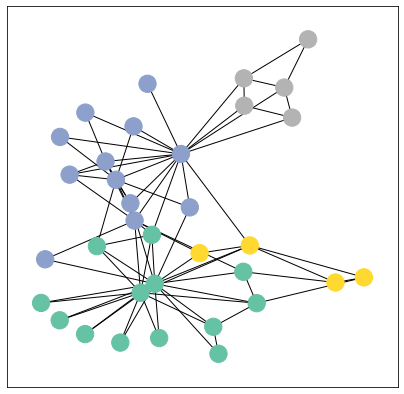
- 연결이 적은 노드 (Low-degree Node): 소수의 이웃으로부터 정보를 받아 상대적으로 자신의 고유 특징을 강하게 유지한다.
- 연결이 많은 노드 (High-degree Node / Hub Node): 다수의 이웃으로부터 정보를 받아 더 복합적이고 풍부한 정보를 표현하게 된다. 이 노드들은 그래프 내에서 정보가 모이고 퍼져나가는 '허브(Hub)' 역할을 수행한다.
GCN은 이를 해결하기 위해 정규화(Normalization) 메커니즘을 내장하고 있다. 이는 연결이 많은 노드의 영향력은 줄이고 연결이 적은 노드의 영향력은 키워 정보 흐름의 균형을 맞추는 역할을 한다. 이 정규화 기법 덕분에 허브 노드는 다양한 정보를 효율적으로 취합하면서도 자신의 고유 정보를 완전히 잃지 않아, 전체 네트워크가 안정적으로 학습을 진행할 수 있게 된다.
GCN의 컨볼루션 연산은 이미지 처리에 사용되는 CNN(Convolutional Neural Network)의 컨볼루션과 개념적으로 유사하지만, 처리하는 데이터의 구조에서 근본적인 차이가 있다.
요약하자면, CNN은 고정된 이웃 관계를 갖는 정형 데이터에 최적화되어 있고, GCN은 이웃의 수와 관계가 모두 다른 비정형 그래프 데이터의 특징을 추출하는 데 특화되어 있다.
GCN에서 홉(Hop)은 정보가 그래프를 따라 얼마나 멀리 퍼져나가는지를 의미한다. 층을 깊게 쌓을수록 노드는 더 넓은 범위의 그래프 구조를 인식하게 된다.
import torch
from torch_geometric.nn import GCNConv
from torch_geometric.data import Data
# 노드 특징 (4개 노드, 각 2개 특징)
x = torch.tensor([[-1, 1], [0, 2], [1, 3], [2, 4]], dtype=torch.float)
# 엣지 연결 정보 (양방향)
edge_index = torch.tensor([[0, 0, 1, 1, 2, 3],
[1, 2, 0, 2, 0, 1]], dtype=torch.long)
# 그래프 데이터 객체
data = Data(x=x, edge_index=edge_index)
print("--- 초기 노드 특징 ---")
print(data.x)
gcn_layer1 = GCNConv(2, 4)
h1 = gcn_layer1(data.x, data.edge_index)
print("\n--- 1-Hop 연산 후 노드 특징 ---")
# 0번 노드는 [기존 0번, 1번, 2번] 특징이 혼합된 결과를 가짐
print(h1)
이 단계에서 각 노드는 자신의 로컬 이웃 정보만을 반영한다.
1-hop 결과를 입력으로 하여 GCN 레이어를 한 번 더 통과시키면, 정보의 수용 범위(Receptive Field)가 이웃의 이웃까지 확장된다.
gcn_layer2 = GCNConv(4, 8)
h2 = gcn_layer2(h1, data.edge_index)
print("\n--- 2-Hop 연산 후 노드 특징 ---")
# 0번 노드는 1번의 이웃인 3번 노드의 정보까지 간접적으로 전달받음
print(h2)
GCN은 반복적인 정보 혼합과 정규화 과정을 통해 그래프 내 노드들의 관계성과 구조적 맥락을 학습한다. 이는 고정된 격자 구조를 가정하는 CNN과 달리, 불규칙하고 복잡한 관계를 갖는 데이터에서 패턴을 발견하는 데 매우 효과적인 방법론이다. GCN의 홉(레이어) 수는 노드가 얼마나 넓은 범위의 정보를 받아들일지를 결정하는 핵심 요소로 작용한다.
GCN(Graph Convolutional Networks. GNN-Graph Neural Network)
GCN은 용어 그대로 CNN개념을 행렬로 보았을때 바로 인접되지 않은 데이터에대한 특징을 추출할 수 있는 필터 역할을 한다.
CNN feature map visualization (link)
GCN은 다음 그림 우측과 같이 인접되지 않은 그래프 형식의 데이터에서 특징을 추출할 때 유용한다.
일반적으로, CNN은 데이터를 구성하는 텐서의 인접 요소에서 특징을 수집해, 특징 벡터를 생성한다.
CNN(Thomas Kipf, Topics in AI (CPSC 532S): Multimodal Learning with Vision, Language and Sound. Link)
그래프 형식 데이터는 이런 방식이 불가능하므로, 다음과 같은 인접행렬을 구성해, 그래프 요소간 연결성을 정의하고, 주변 인접 데이터와 관계를 포함한 특징을 계산해야 한다.
Adjacency Matrix (link)
다음 우측 그림에서 적색 노드 근처 인접된 노드의 특징을 수집해 특징 벡터를 계산해야 한다면, kNN으로 알려진 인접 노드들을 탐색한 후, 인접 행렬을 구성해야 한다. 다음 수식에서 Ni는 이웃 노드 인덱스, Cij는 정규화를 위한 팩터, h는 노드의 특징 벡터, l은 노드 인덱스를 의미한다.
CNN(Thomas Kipf, Link)
Node, Link, Graph prediction
GCN은 노드, 링크로 구성되는 그래프 데이터에 대한 학습이 가능하다. 다음은 학습된 모델을 통해, 가능한 데이터 분류, 에측, 재구성 등의 사례를 보여준다.
GNN based classification(Zongham al et, 2019)
GNN based reconstruction(Zongham al et, 2019)
GDL(Geometric Deep Learning)
GDL은 GCN을 이용해 기하학적 딥러닝 모델을 정의할 수 있음을 설명하는 용어이다. 분자 구조, 다차원 포인트 등은 결론적으로 기하학적으로 다차원 요소간의 관계를 표현한 그래프 구조이다. GDL은 가장 떠오르는 딥러닝 분야 중 하나이다.
Non-Euclidean Data(Flawnson Tong, 2019, What is Geometric Deep Learning?)
다차원 데이터를 학습하는 것은 쉽지 않다. 최근 이 기술과 관련된 컨퍼런스가 개최되었다.
PyTorch Geometry 라이브러리는 화학 분자 모델과 같은 위상 그래프 형식 데이터셋을 딥러닝 방식으로 학습, 계산, 분류, 해석하기 위해 개발된 오픈소스로 많이 활용되고 있다.
이외 다른 오픈소스 라이브러리는 다음 링크를 참고한다.
Practice
GCN과 유사한 개념 사용 사례로, 다음과 같이 스캔된 3차원 데이터셋을 분류하는 PointNet 딥러닝 모델이 있다. 스캔된 포인트 클라우드 해석도 그래프 모델로 분석할 수 있다.
포인트 클라우드의 각 포인트는 화학 분자처럼 특징을 가지고, 포인트 간의 관계를 가진다. 이를 통해, 제시된 포인트 집합이 어떤 종류인지 해석 및 예측할 수 있다. 이는 화학 분자식을 이용해 어떤 단백질인지 예측하는 사례와 개념적으로 동일하다.
다음 표시된 링크에 실행 코드를 확인할 수 있다.
PointGNN은 포인트 클라우드 세그먼테이션에 GNN을 사용한다.
다음은 GNN 관련 유명예제인 카라테 쇼셜 클럽 그래프 데이터를 학습하고 예측하는 예제이다.
Kerate club classification (colab)
그래프 데이터로 표현된 분자 모델들을 학습해, 용해도를 예측한다. 학습 모델에 목적에 맞게 다양한 분류, 복원이 가능하다(분자 모델 구조에서 향기 분류, 강도 등 분석 예측. 모델 구조 재구성 등).
다음은 심장독성 특징이 있는 화학물 분자구조를 예측하는 모델 예이다.
TF-GNN (kaggle)
Conclusion
이 글은 GCN, GDL의 개념, 사용 라이브러리, 응용 사례에 대해 정리해 보았다. GCN은 아직 이미지, 자연어 딥러닝 분야에 비해 발전 속도가 느리다. 데이터셋 한계, 대용량 데이터셋 이슈, 계산 과정의 복잡성 등의 문제가 있지만, 오픈소스 커뮤니티를 통해 이런 문제가 해결되고 있는 중이다. 이 분야는 하드웨어 성능 개선과 더불어 꾸준히 발전할 것이다.
Reference
- Zongham al et, 2019, A Comprehensive Survey on Graph Neural Network
- Machine Learning for Scent: Learning Generalizable Perceptual Representations of Small Molecules
- Shanon Hong, 2020, An Introduction to Graph Neural Network(GNN) For Analysing Structured Data (link. Korean version)
- Flawnson Tong, 2019, What is Geometric Deep Learning? (link)
- Michael Bronstein, 2021, Geometric foundations of Deep Learning (link)
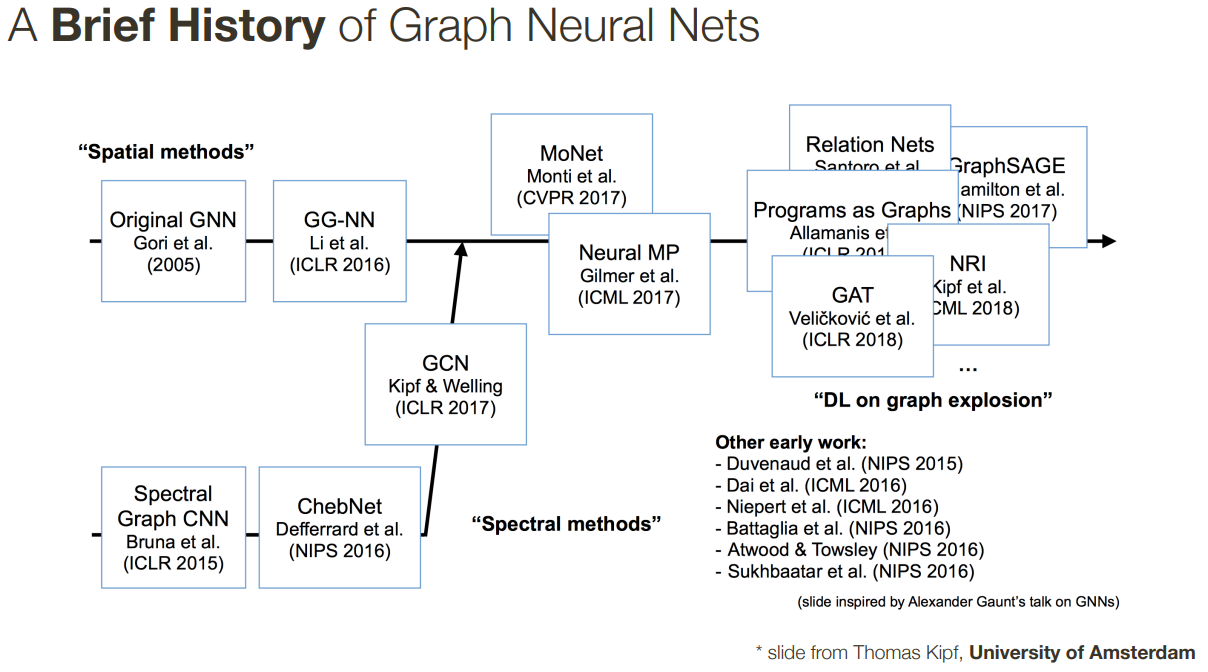
- Thomas Kipf, Topics in AI (CPSC 532S): Multimodal Learning with Vision, Language and Sound. Link
- 3D-SegNet(2020) and PointSIFT(2018)
- THOMAS KIPF, 2016, GRAPH CONVOLUTIONAL NETWORKS (link)
- An autonomous laboratory for the accelerated synthesis of novel materials | Nature
댓글 없음:
댓글 쓰기