Daddy Makers: 대중화된 멀티모달 생성AI 모델, Stable Diffusion 아키텍처 분석과 동작 원리 이해

이 글은 Stable Diffusion(스테이블 디퓨전) 아키텍처를 분석하고, 핵심 개념과 모델을 이해한다. 스테이블 디퓨전은 기존에 연구된 멀티모달(Multi Modal) 딥러닝 아키텍처인 CLIP(OpenAI), 노이즈 확산(디퓨전) 및 역확산 시뮬레이션 모델, 컴퓨터 비전에서 사용되던 U-Net, 오토인코더를 통한 데이터 압축과 잠재공간(Latent Space)차원 연산 등을 적극 사용해, Text to Image 생성AI(Gen AI) 기술을 구현한다.

스테이블 디퓨전은 text-to-image 생성AI 모델로 RunwayML, Stavility AI의 지원을 받은 뮌헨하이델베르그 대학 CompViz 그룹에서 개발해 동작 원리와 소스 전체를 공개하였다(2022.8. GitHub). 이 모델은 대중의 폭팔적인 관심을 끌며 대중에 생성AI를 각인시켰고, 이 기술을 이용한 멀티모달 생성AI(Gen AI)기술 투자의 기폭제가 되었다. 2023년에는 빅테크 기업 OpenAI, Microsoft, Google, Meta(Facebook), NVIDIA가 생성AI에 큰 투자를 했고, 그 결과 우리는 Microsoft CoPilot(LLM. Text-Image), OpenAI의 ChatGPT4(LLM. Text-Image), SORA(Text-Video), Google Gemini, Facebook LLAMA(LLM), ImageBind(Text-Image-Sound-Video)와 같은 생성AI 기술을 사용할 수 있게 되었다.

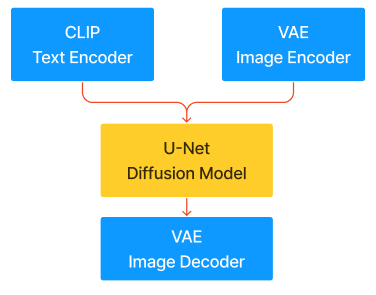
스테이블 디퓨전은 다음 그림과 같이 디퓨전 모델, U-Net, 오토인코더(Autoencoder), 트랜스포머(Transformer) 어텐션 모델(Attention)을 사용해, 학습한 모델을 역으로 계산해 주어진 텍스트 조건에서 이미지가 생성될 수 있도록 한다.

스테이블 디퓨전 아키텍처 기반 Text To Image 생성(Inference) 및 학습 과정

이 모델은 기존 자연어 처리 분야에서 개발된 트랜스포머, 컴퓨터 비전 딥러닝 모델 기술을 적극 사용한다. 이와 관련된 내용을 깊게 이해하고 싶다면 다음을 참고한다.

실제 코드 개발 방법을 알고 싶다면, 다음 링크를 참고한다.

파이토치로 멀티모달 생성AI 모델, Stable Diffusion 아키텍처를 코딩, 구현해보기

스테이블 디퓨전 아키텍처 모델의 이해가 아닌, 설치 및 사용 방법만 알고 싶을 때는 아래 링크를 참고한다.

이 글은 멀티모달, 디퓨전과 관련된 다양한 문헌을 참고해 정리된 것이다. 관련 내용은 이 글의 레퍼런스를 참고한다.

아키텍처 구조

스테이블 디퓨젼은 기존에 개발된 디퓨젼(Diffusion), 벡터 임베딩(Vector Embedding), U-Net과 VAE(Variational Autoencoders), 오토인코더, 트랜스포머와 CLIP을 활용해 개발된 것이다. 스테이블 디퓨전 2는 기존 CLIP을 그대로 사용하지 않고, 입력된 텍스트를 조건으로 파라메터로 조정할 수 있도록 하였다(컨디셔닝 기법 적용). 이로 인해, 입력 텍스트에 따라 이미지 스타일을 변화시킬 수 있다. 다음 그림은 스테이블 디퓨전의 핵심기술요소만 보여준다.

스테이블 디퓨전 아키텍처

스테이블 디퓨전에 텍스트가 입력되면, 텍스트 인코더가 특징을 가진 임베딩 벡터로 변환한다. 아울러, 이미지-노이즈 데이터셋으로 학습된 디퓨전 모델이 사용되어, 텍스트 임베딩 벡터와 압축된 이미지 벡터가 잠재공간(Latent Space)에 표현된다. 트랜스포머를 이용해, 유사도가 제일 큰(잠재공간에서 가까운 텍스트-이미지 쌍) 텍스트-이미지 임베딩 벡터 쌍을 계산한다. 이 결과로 이미지 특징 벡터를 얻고, 오토인코더로 특징 벡터를 이미지로 변환한다.

참고로, 유명한 딥러닝 플랫폼 개발사인 MosaicML에서 공개한 스테이블 디퓨전 개발 과정(2023.4.26. 참고-MosaicML의 Stable Diffusion 소스코드)은 의미있는 정보를 제공한다. 이 사례에서 Stable Diffusion 개발 시 GPU 사용 비용은 NVIDIA A100 GPU x 100개 x 1.6일, x 4.9일 동안 550,000 학습량이다. 총 23,835 A100 시간이 필요하다. 100TB 데이터셋이 학습에 사용되었다. 이를 비용으로 환산하면 $47,700 (약 6천만원) 정도가 된다. 즉, 그라운드 제로에서 스테이블 디퓨전 모델을 학습한다는 것은 어느 정도 규모와 자원이 있어야 한다는 것을 의미한다(이 과정을 Automatic1111의 WebUI와 같은 도구를 이용해 스테이블 디퓨전 모델을 커스텀 데이터셋으로 전이학습하는 것과 혼동하지 말자).

MosaicML의 Stable Diffusion Github(소스코드)

디노이즈와 디퓨전

스테이블 디퓨전(Diffusion)에서 디퓨전은 텍스트에서 이미지를 생성하는 변환기 역할을 한다. 디퓨전 모델을 사용하여, 기존 생성AI 모델인 GAN(Generative Adversarial Network)과 같이 암시적으로 데이터를 학습하지 않고, 점진적이고 안정적으로 노이즈를 지워 새로운 샘플 이미지를 생성한다. GAN방식 대신 디퓨전을 사용하고자 했던 개발자들의 핵심 질문은 다음과 같다.

어떻게 무작위 이미지(데이터)에서 안정적이고 고품질 이미지를 생성, 학습할 수 있을 까? 어떻게 랜덤하게 분산된 데이터를 분산되기 전의 모습으로 되돌릴 수 있을까?

이 질문은 어떻게 생성해야할 이미지의 통계적 분포를 효과적으로 학습할 수 있는가를 묻고 있는 것이다. 기존의 GAN은 생성자, 판별자를 통해 암시적으로 이 분포를 학습하였으나, 오버피팅(Overfitting), 모드 붕괴(Mode Collapse. 다양한 입력 데이터 특징이 학습되지 않아, 치우친 결과만 얻는 현상)와 같은 불안정한 부분이 있었다. GAN은 학습을 통해 안정적으로 해를 수렴한다고 보장하기 어렵다. GAN은 입력 데이터의 통계적 분포가 정규분포같이 다양성이 있지 않으면 붕괴(발산)될 수 있다.

GAN의 모드 붕괴 현상 (MNIST 데이터 학습이 계속되어도 입력에 대해 동일한 결과만 얻음)

스테이블 디퓨전은 여기에 다음 질문을 덧붙인다.

어떻게 생성될 이미지의 조건을 텍스트로 조정할 수 있을까?

이건 멀티모달리티(Multi-modality) 조건을 어떻게 구현할 수 있는가? 즉, 텍스트 입력 조건에 따라 연관된 다른 형태의 데이터를 어떻게 생성할 수 있느냐는 것이다.

우선, 첫번째 질문은 디퓨전(확산) 현상과 관계된다. 디퓨전은 노이즈의 확산(디퓨전)을 의미한다. 이와 유사한 연구가 오래전 물리학 분야에서 있었다. 노이즈가 이미지 전체에 확산되는 과정은 분자운동에 의해 충돌하며 퍼지는 엔트로피 현상과 유사하다(브라운 운동으로 알려져 있음). 물리학자는 이 현상을 확산 물질 밀도가 변화하는 속도를 시간과 위치에 의한 편미분함수로 정의할 수 있음을 증명했다. 이 함수는 미세입자 동역학 해석을 위해 개발된 랑주뱅 동역학 모델(Langevin equation, 1908)에서 설명되었다(아래 자료 참고. 특정 상황에서는 열 방정식으로 해석).

브라운 운동(Brownian Motion - Learn Physics From The Physics Authority)과 확산 방정식(Brownian motion's diffusion equation. Diffusion Equation - Derivation and Explanation using Brownian)

스테이블 디퓨전은 이 개념을 생성AI에 사용한다. 디퓨전 모델은 다음의 순방향 노이즈 확산 방정식으로 시작한다.

여기서,

x(t) = 잡음

t = 확산시간

σ(t) = 잡음강도

Δt = 확산단위시간

r≈N(0,1) = 표준 정규 확률 변수

방정식의 의미는 단위시간이 지날수록 이전 잡음 수준에 비례하고, 표준정규확률에 따라 잡음강도가 비례하여, 노이즈가 증가한다는 것이다(당연하다). 만약, 1차원 공간에서 이를 그대로 코딩한다면, 다음과 같을 것이다.

x[i + 1] = x[i] + random_normal * noise_strength

이를 역방향으로 되돌릴 수 있다면, 임의의 노이즈된 데이터에서 원본 이미지를 생성할 수 있다.

이를 위해, 전방향 확산 방정식을 미분방정식으로 변환하여 역확산 방정식을 유도한다(딥러닝 모델의 가중치는 함수의 미분값을 반복적으로 조정하는 과정임을 떠올리자). 이를 수식으로 표현하면 다음과 같다(유도과정 참고).

수식은 전체 고정된 T 시간을 가정해, 유한하게 계산되도록 한다. 수식 의미는 다음과 같다.

t + Δt 의 잡음 x()는 이전 시간의 잡음 x(t)에 비례한다(첫번째항). 아울러, 잡음강도 σ(T - t) 제곱에 비례하는 데, 이는 잡음 확률을 나타내는 함수 log p(x) 함수의 미분값과 Δt에 비례한다(두번째항). 또한, 잡음강도 σ(T - t), Δt, 정규확률분포 r에 비례한다. 두번째 항을 간략히 표현하면, s(x, t) 함수로 정리된다. 여기서, s(x, t) 함수를 diffusion score 함수라 한다.

다음 그림은 x함수 값의 전방향, 역방향 확산 과정을 t시간에 따라 출력한 것이다.

전방향(좌), 역방향(우) 확산 함수 x(t) 결과(Score-Based Generative Modeling through Stochastic Differential Equations)

전확산, 역확산 시뮬레이션은 다음과 같이 구현 될 수 있다.

def noise_strength_constant(t): # 노이즈 강도 함수 리턴값은 1로 설정

return 1

def forward_diffusion_1D(x0, noise_strength_fn, t0, nsteps, dt):

x = np.zeros(nsteps + 1) # 시간에 대한 노이즈 샘플 흐름을 담기 위한 벡터 생성

x[0] = x0 # 초기 x0 샘플 설정

t = t0 + np.arange(nsteps + 1) * dt # 샘플링되는 t시간 계산

for i in range(nsteps): # 디퓨전 시뮬레이션(Euler-Maruyama 식 사용)

noise_strength = noise_strength_fn(t[i]) # t시간 잡음 강도

random_normal = np.random.randn() # 정규분포 잡음

x[i + 1] = x[i] + random_normal * noise_strength # 각 시간마다 잡음 계산

return x, t # 잡음 벡터, 해당 시간 시점 리턴

여기서,

x0: 초기 샘플 데이터값
noise_strength_fn: 노이즈 강도 함수. 시간 t입력.
t0: 초기 시간 단계
nsteps: 확산 단계
dt: 시간 미분치
x: nstep * dt 시간의 노이즈 샘플값(벡터) 리턴
t: nstep * dt 시간 리턴

이다.

순방향 확산을 앞서 정의된 함수로 시뮬레이션해본다.

nsteps = 100 # 확산 최대 단계 N

t0 = 0 # 초기 시간

dt = 0.1 # 단위 시간

noise_strength_fn = noise_strength_constant # 노이즈 강도

x0 = 0 # 초기 샘플링 값

num_tries = 7 # 가시화할 단계수

# 확산 그래프 출력

plt.figure(figsize=(15, 5))

for i in range(num_tries): # 확산 시뮬레이션

x, t = forward_diffusion_1D(x0, noise_strength_fn, t0, nsteps, dt)

plt.plot(t, x, label=f'Trial {i+1}') # 확산값 출력

plt.xlabel('Time', fontsize=20)

plt.ylabel('Sample Value ($x$)', fontsize=20)

plt.title('Forward Diffusion Visualization', fontsize=20)

plt.legend()

plt.show()

결과는 다음과 같다.

이제 역방향 확산 함수를 구현한다.

앞서 설명한 바와 같이, 순방향은 정규분포를 이용할 수 있지만, 역방향은 이를 그대로 사용할 수 없어, 다음 편미분 방정식으로 근사화해 구현한다.

여기서, s(x, t)는 score 함수로 알려져 있다. 이를 구현할 수 있다면, 역방향 확산이 가능하다. 시작점 x0=0이고, 잡음 강도가 일정하다면, s() 함수는 다음과 같다.

이를 코드로 다음과 같이 구현한다.

def score_simple(x, x0, noise_strength, t):

score = - (x - x0) / ((noise_strength**2) * t) # s(x,t) 스코어 함수

return score

def reverse_diffusion_1D(x0, noise_strength_fn, score_fn, T, nsteps, dt):

x = np.zeros(nsteps + 1) # 잡음 경로 벡터 리스트

x[0] = x0 # 잡음 초기값

t = np.arange(nsteps + 1) * dt # 잡음 생성 시점 계산

# Euler-Maruyama 식 사용해 역확산 시뮬레이션

for i in range(nsteps):

noise_strength = noise_strength_fn(T - t[i]) # 노이즈 강도

score = score_fn(x[i], 0, noise_strength, T - t[i]) # s(x,t) 스코어 함수

random_normal = np.random.randn() # 랜덤값

x[i + 1] = x[i] + score * noise_strength**2 * dt + noise_strength * random_normal * np.sqrt(dt) # 잡음 역확산

return x, t

이제, 시뮬레이션하여, 출력해 본다.

nsteps = 100

t0 = 0

dt = 0.1

noise_strength_fn = noise_strength_constant

score_fn = score_simple

x0 = 0

T = 11

num_tries = 7

plt.figure(figsize=(15, 5))

for i in range(num_tries):

x0 = np.random.normal(loc=0, scale=T) # 타임T, 강도1 랜덤값

x, t = reverse_diffusion_1D(x0, noise_strength_fn, score_fn, T, nsteps, dt)

plt.plot(t, x, label=f'Trial {i+1}')

plt.xlabel('Time', fontsize=20)

plt.ylabel('Sample Value ($x$)', fontsize=20)

plt.title('Reverse Diffusion', fontsize=20)

plt.legend()

plt.show()

역확산 효과가 잘 시뮬레이션되었다.

이런 개념을 이용하면, 순방향 디퓨전, 역방향 디퓨전 방식을 이용해, 다양하고 복잡한 이미지(노이즈)에서 원본 이미지로 변환하거나, 반대로 역변환할 수 있다(참고. Score-Based Generative Modeling, 2011).

확률적 미분 디퓨전 방정식(SDE. Stochastic Differential Equation) 모델(Fareed Khan, 2024. Score-Based Generative Modeling, 2011)

이 역변환 디퓨전 방정식은 디노이징 디퓨전 모델(Denoising Diffusion Model)이라 불린다. 디노이징 디퓨전 모델은 DDPM(Denoising Diffusion Probabilistic Models)기술로 알려져 있고(Jonathan Ho et al, 2020), 스테이블 디퓨전에서 적극 사용된다(참고 - 소스코드).

DDPM(Denoising Diffusion Probabilistic Models. Jonathan Ho et al, 2020)

디퓨전 함수를 이미지 데이터에 적용하면, t 시간에 따른 노이즈 양을 조정할 수 있다. 다음 그림은 그 과정을 보여준다. 디퓨전 함수에 t0를 입력하면 원본 이미지, T를 입력하면, 노이즈 이미지가 계산된다.

노이징(Noising) 및 디노이징(Denoising) 과정 개념(Jay Alammar, 2022)

U-Net과 디퓨전

전방향 역방향 디퓨전 함수의 대상은 이미지가 되어야 한다. 픽셀 공간을 다른 픽셀 값으로 변환하는 것이기 때문에, 이미지의 입력 픽셀이 라벨링된 출력 픽셀로 계산되어야 한다. 그러므로, 이 기능은 이미지 세그먼테이션에 많이 사용된 U-Net 모델을 사용한다. 디퓨전 함수와 U-Net을 통해, 노이즈-이미지 간 변환 및 역변환 맵핑을 하도록 설계한다.

디퓨전은 시간의 함수이므로, 주어진 데이터의 해를 점진적으로 학습(가중치 조정)할 수 있게 되고, 이는 스테이블한(안정적인) 학습 모델을 얻을 수 있다는 것을 의미한다. 디퓨전 함수를 이용해 각 에폭(Epoch) 당 학습할 다양한 잡음 있는 데이터셋을 만든다. s(x, t)에서 t값을 임의로 할당해, 입력 이미지에 다양한 변형을 하여, 미니배치 데이터를 생성한다. 다음 그림은 이를 보여준다.

UNet에 입력되는 학습 데이터셋(Steins, 2023)

각 학습 단계는 다음과 같은 순서로 진행된다.

t 시간 단계 임베딩 벡터 변환
t 시간에 따른 노이즈 이미지 생성
1, 2를 입력데이터, 노이즈를 라벨링 데이터로 하여, U-Net 모델 학습

입력 이미지-텍스트 학습 데이터를 노이즈 이미지 라벨으로 학습하고, 역계산하는 방식으로 이미지를 생성한다. 다음 그림은 이를 보여준다.

디퓨전에서 사용하는 U-Net 구조와 역할(Steins, 2023)

참고로, U-Net은 입력 픽셀 값을 압축해 일반화(추상화)하여, 라벨링된 픽셀 값으로 계산하는 학습 모델로 딥러닝 컴퓨터 비전 분야에서 이미지 세그먼테이션에서 사용되었다. 다음은 32x32 이미지를 목표 라벨 이미지로 학습하기 위한 U-Net 모델을 보여준다. 일반화된 이미지 특징 학습으로 인해, 이미지 세부 특징을 놓칠 수 있어, 각 계층마다 ResNet 잔차연결을 사용한 것을 확인할 수 있다.

U-Net과 ResNet 모델 구조(Seachaos, 2023)

잠재공간과 오토인코더

입력 이미지를 그대로 디퓨전과 U-Net으로 계산한다면, 이미지 크기에 따라 매우 큰 GPU 메모리와 계산 성능이 필요할 것이다. 이를 잠재공간(Latent Space)에서 표현하면, 메모리와 연산량을 크게 줄일 수 있다.

잠재공간은 데이터 특징이 압축된 벡터를 표현하는 다차원 공간이다. 이 공간은 입력 데이터가 압축된 벡터로 차원을 가진다. VAE(Variational Autoencoder. 변분 오토인코더)를 사용하면, 데이터를 압축해 잠재공간에 위치시킬 수 있다. 잠재 공간에서 학습한다면, 원본 이미지보다 훨씬 작은 임베딩 벡터 데이터만 계산되므로, 개선된 연산 속도과 효율적인 GPU 메모리 사용이 가능하다. 이를 위해, VAE는 다음 그림과 같이 인코더-디코더 레이어를 배치하고, 잠재공간으로 압축된 텐서 출력의 평균μ, 분산σ이 정규분포를 가지는 확률분포 N(μ, σ)가 학습되도록 한다.

VAE 오토인코더 모델과 잠재공간(Latent Space)

오토인코더 구현은 단순히 신경망 층으로 인코더와 디코더를 만들고, 인코더의 결과가 확률분포 N(μ, σ)가 되도록 학습하는 것이다. 다음은 파이토치로 구현한 핵심 코드 일부를 보여준다.

class VAE(nn.Module):

def __init__(self, input_dim=784, hidden_dim=400, latent_dim=200, device=device):

super(VAE, self).__init__()

self.encoder = nn.Sequential(

nn.Linear(input_dim, hidden_dim),

nn.LeakyReLU(0.2),

nn.Linear(hidden_dim, latent_dim),

nn.LeakyReLU(0.2)

) # 인코더. 선형 레이어 + ReLU의 조합이다.

# 잠재공간 차원(평균, 편차)로 인코더 출력을 맵핑

self.mean_layer = nn.Linear(latent_dim, 2)

self.logvar_layer = nn.Linear(latent_dim, 2)

self.decoder = nn.Sequential(

nn.Linear(2, latent_dim),

nn.LeakyReLU(0.2),

nn.Linear(latent_dim, hidden_dim),

nn.LeakyReLU(0.2),

nn.Linear(hidden_dim, input_dim),

nn.Sigmoid()

) # 디코더는 인코더 반대로 처리함.

def encode(self, x): # 인코더 계산

x = self.encoder(x)

mean, logvar = self.mean_layer(x), self.logvar_layer(x)

return mean, logvar

def reparameterization(self, mean, var): # 정규분포 계산

epsilon = torch.randn_like(var).to(device)

z = mean + var*epsilon

return z

def decode(self, x): # 디코더 계산

return self.decoder(x)

def forward(self, x):

mean, logvar = self.encode(x) # 인코더 학습

z = self.reparameterization(mean, logvar) # 정규분포 계산

x_hat = self.decode(z) # 디코더 계산

return x_hat, mean, logvar # 계산결과, 평균, 분산

def loss_function(x, x_hat, mean, log_var): # 손실 함수 정의

reproduction_loss = nn.functional.binary_cross_entropy(x_hat, x, reduction='sum') # 이진 교차엔트로피 손실

KLD = - 0.5 * torch.sum(1+ log_var - mean.pow(2) - log_var.exp()) # Kullback-Leibler(KL) 손실 계산

return reproduction_loss + KLD # 두 확률분포의 거리를 최소화하려는 의도

오토인코더를 이용해, 다음 그림과 같이 압축된 잠재공간차원의 특정 위치는 입력된 데이터를 맵핑할 수 있다.

잠재공간에 맵핑된(인코딩된) 데이터(Alexej Klushyn, 2019.12, Learning Hierarchical Priors in VAEs)

잠재공간에서 디퓨젼을 수행하는 과정은 앞의 픽셀공간에서 디퓨전을 실행하는 것과 유사하다(디퓨전 방정식은 특정 데이터 유형과 무관하게 동작됨). 노이즈-이미지 간 디퓨전은 오토인코더 모델을 이용한다. 오토인코더는 인코더-디코더 쌍을 가지고 있다. 그러므로, 전방향으로 노이즈 라벨을 예측하고, 역방향으로 노이즈에서 이미지를 생성하는 것이 가능하다.

텍스트 인코더도 같은 방식으로 잠재공간차원에 맵핑한다. 참고로, 변환된 텍스트 벡터를 임베딩 벡터라 한다(정확히는 벡터가 아닌 텐서값).

이제, 오토인코더로 잠재공간에 압축되어 위치된 입력 데이터에 텍스트 조건정보를 추가해 파라메터화하고, 이에 따라 이미지가 생성될 수 있도록 U-Net모델을 학습한다. 이를 컨디셔닝이라 한다. 컨디셔닝은 학습 시 특정 조건을 줄 수 있는 파라메터(예. 텍스트)를 포함한다.

잠재공간에서 디퓨전 컨디셔닝 처리(Steins, 2023)

입력 데이터(이미지)와 텍스트를 잠재 공간차원에서 거리가 가깝도록 유사도를 조정해야(학습해야) 하므로, 앞에 글에서 언급한 트랜스포머의 어텐션 모델을 사용한다.

컨디셔닝은 트랜스포머 모델을 통해, 각 U-Net의 레이어 모듈에 출력과 연결되도록 한다. 이를 통해, 신경망은 입력 이미지와 텍스트에 대해 다양한 x(t)에 대한 노이즈 배치 데이터를 예측하도록 학습될 것이다.

학습이 끝나면, 텍스트와 노이즈를 입력해 잠재공간 차원에서 노이즈 역확산 방정식(DDPM. Denoising Diffusion Probabilistic Models. 디노이징 확률 모델)을 계산한다. 이를 통해, 텍스트 입력 조건에 따른 이미지를 생성하도록 한다. 각 U-Net 층에 트랜스포머의 어텐션 모델이 연결하여, 일반적 수준에서 세부적 수준까지 생성되는 이미지를 조건에 따라 생성하도록 한다.

트랜스포머와 CLIP

스테이블 디퓨전은 트랜스포머를 이용해, 멀티모달인 텍스트-이미지 데이터쌍의 유사도를 계산하는 CLIP(Contrasive Language-Image Pre-Traning. 참고)을 사용한다. CLIP을 이용하면, 'lovely cat'과 고양이 이미지 임베딩 벡터를 잠재 공간 차원에서 거리가 가까워지도록 조정할 수 있다. 즉, 다음과 같은 W 가중치를 학습할 수 있다.

i ≈ t·W

여기서,

i=image embedding vector

t=text embedding vector

W=weight vector

이때, 목적 함수는 cosine similarity(유사도)가 된다(트랜스포머 모델에서 사용된 어텐션 스코어 행렬값). CLIP을 이용해, 멀티모달 데이터셋인 텍스트-이미지를 잠재공간에 표현해, 멀티모달(Multi Modal. 쉽게 말해 이종 데이터셋) 조건에서 학습할 수 있도록 한다. 텍스트 임베딩 벡터를 이미지 생성 과정에 포함하려면, 노이즈 예측하는 U-Net 부분을 텍스트 조건에 따라 조정되도록 수정해야 한다. 다음 그림은 이 과정을 보여준다.

스테이블 디퓨전에서 트랜스포머 어텐션을 이용한 U-Net 컨디셔닝(Robin Rombach et al, 2022)

앞의 그림의 QKV는 트랜스포머 어텐션 모델의 Query, Key, Value 입력을 의미한다. 여기서, Query는 조건화를 위해 텍스트 임베딩이 입력되어야 한다. K, V는 학습된 이미지 컨텍스트가 입력되어야 한다. 그럼, 어텐션 모델이 입력되는 이미지, 텍스트의 유사도를 가깝게 만들기 위해 학습 가중치를 조정할 것이다. U-Net 각 층마다 어텐션 모델을 적용하여, 개요에서 상세 수준까지 스타일을 조정할 수 있도록 컨디셔닝을 적용한다.

이제 컨디셔닝 된 U-Net 모델을 설계했으므로, 잠재공간에 표현된 압축 이미지 임베딩 벡터와 노이즈 양을 입력받아, ResNet (잔차연결 모델)을 이용해, 예측된 노이즈 이미지를 생성하도록 학습한다.

이제, 학습될 배치 데이터(입력 이미지, 이미지를 설명하는 텍스트)가 스테이블 디퓨전 모델에입력될 때 마다, 각 ResNet에서 출력되는 이미지 특징 벡터와 입력된 텍스트 벡터 간의 유사도가 가까워지도록 W값이 조정될 것이다. 각 ResNet의 레이어 층별로 어텐션 스코어가 계산되므로, 텍스트-이미지 생성 시 텍스트의 묘사에 따라서, 이미지 전체 및 디테일 생성에 조건을 줄 수 있다.

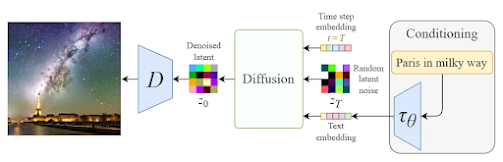
디퓨전(확산) 모델에 따라, 입력 데이터에 대한 다양한 노이즈 이미지가 계산되도록 학습되므로, 학습 결과를 역방향 디퓨전 모델로 역계산하여, 디노이징하면 텍스트 입력에 따른 이미지를 생성할 수 있다.

역확산 모델에 따른 단계별 디노이징 예(Lgnacio Aristimuno, 2023.11, An Introduction to Diffusion Models and Stable Diffusion)

다음 그림은 앞의 과정을 거쳐 개발된 스테이블 디퓨전 아키텍처를 보여준다. 그림에서 디노이징 단계(denoising step)은 스위치(switch)에 의해 역계산되는 것을 이해할 수 있다.

스테이블 디퓨전 아키텍처(Robin Rombach et al, 2022)

마무리

이 글은 멀티모달 생성AI를 대중에 널리 알리게 된 딥러닝 모델인 스테이블 디퓨전의 동작 원리, 모델을 가급적 상세히 분석, 정리해 보았다. 이 과정을 통해, 멀티모달 데이터 생성 과정, 메커니즘, 활용 방법 및 한계를 확인할 수 있다.

앞서 보았듯이 스테이블 디퓨전 개발자들은 오토인코더를 통해 계산된 잠재공간차원에서 U-Net을 조건화하여 모델을 학습하도록 하였다. 입력 텍스트에 대한 조건화된 U-Net학습은 트랜스포머의 어텐션 모델을 적용하여 처리했다. 이런 멀티 모달리티 기능은 OpenAI의 CLIP 아키텍처를 재활용한 것이다. 잠재공간에서 조건화되고 학습될 수 있는 U-Net을 구현한다는 것은 다른 발전 가능성을 내포하고 있다. 잠재공간에 입력될 임베딩 벡터에 비디오 영상 프레임과 시간을 함께 입력해 학습할 수 있을 것이다. 조건화된 파라메터에 CLIP에서 자동생성된 비디오 캡션을 사용하거나, 생성 데이터의 형태와 스타일을 제어할 수 있는 파라메터를 텍스트처럼 입력하고 학습할 수도 있다.

CLIP으로 촉발된 멀티 모달리티와 스테이블 디퓨전 아키텍처의 확장 가능성은 생성AI의 기술 발전을 증폭시키고 있다.